By CMS Collaboration

 

The 2012 discovery of the Higgs boson at the CERN LHC was a milestone confirmation of the Standard Model, a theoretical framework that describes all the known elementary particles – the fundamental building blocks of our universe – and their interactions. Theorists first predicted a Higgs boson in a trio of 1964 “PRL papers,” one of which is Broken Symmetries and the Masses of Gauge Bosons written by Peter W. Higgs. The paper’s name is suggestive; Higgs and his colleagues Robert Brout and François Englert identified a mechanism by which the elementary particles acquire mass through interactions with a “Higgs field.” If this sounds abstract, don’t worry—it is. The real-world consequences, however, are staggering; the Brout-Englert-Higgs mechanism predicted the existence of one more particle, a so-called Higgs boson, whose properties are to date perfectly consistent with the Higgs boson observed at the LHC. This is a beautiful example of harmony between theory and experiment—not always the case in science—and Peter Higgs and François Englert were awarded the 2013 Nobel Prize in Physics for their predictions.

You might ask: why is there only one Higgs boson? Couldn’t there be more? The answer is yes, there certainly could be. In fact, the Standard Model Higgs sector is the simplest possibility required for consistency with experiment. Many extensions to the Standard Model, collectively called Beyond the Standard Model theories, have extended Higgs sectors predicting multiple Higgs bosons. These Beyond the Standard Model theories are introduced because they extend the phenomenology, or descriptive power, of the Standard Model. This is well motivated by known shortcomings of the Standard Model. Let’s look at an example:

Two Higgs Doublet Models (2HDMs), as their names suggest, double the structure in the Higgs sector, ultimately predicting five (!) Higgs bosons. One of the most frequently-cited reasons to study 2HDMs is that the Higgs sector of a minimal version of the Supersymmetric Standard Model must itself be a 2HDM. What? Let’s unpack that.

Supersymmetry is a Beyond the Standard Model theory–really a vast family of theories–that postulates the existence of heavy superpartner particles (sparticles for short) paired with each Standard Model particle. For instance, the electron has a selectron and the photon has a photino. The partners are opposites, in the sense that every fermion has a bosonic superpartner and every boson has a fermionic superpartner. Sparticles are heavier than their Standard Model counterparts and have not been discovered to date.

The allure of supersymmetry lies in its potential to solve some of the greatest mysteries in physics. For example, it provides an excellent candidate for dark matter, an invisible substance that makes up about a quarter of the mass of our universe. It could also help unify the fundamental forces of nature and stabilize calculations related to the Higgs boson, which is important for understanding why particles have mass.

Despite its elegance, supersymmetry remains a hypothesis and has not yet been observed. If discovered, though, supersymmetry would revolutionize our understanding of the universe, opening a new chapter in the epic story of particle physics.

If our universe truly is supersymmetric, we must observe new Higgs bosons. This motivated our team to search for one of the additional Higgs bosons predicted in 2HDMs, a particle called A, in its decay to the Z boson and the presently-observed Higgs boson h. Summarily, this process is A→Zh. The Z boson decays roughly 7% of the time to pairs of light leptons, either electrons (e+e-) or muons (μ+μ-). These light leptons are observable in our detector and give us a clean experimental signature to reference, or trigger on. Once we identify an ensemble of events consistent with Z boson decays, we then have to determine which events also contain h. To do so, we search for h decays to tau leptons 𝜏+𝜏- (this occurs roughly 6% of the time). The reason is that 𝜏 particles themselves decay and appear in the detector as either light leptons (e, μ) or showers of hadrons (𝜏h, where the “h” subscript indicates “hadronic”). The light leptons are cleanly identified in the detector, and while 𝜏h are more challenging, advances and machine learning have drastically improved our ability to detect them. As a shorthand, the full decay we aim to identify is A→Zh→ll𝜏𝜏.

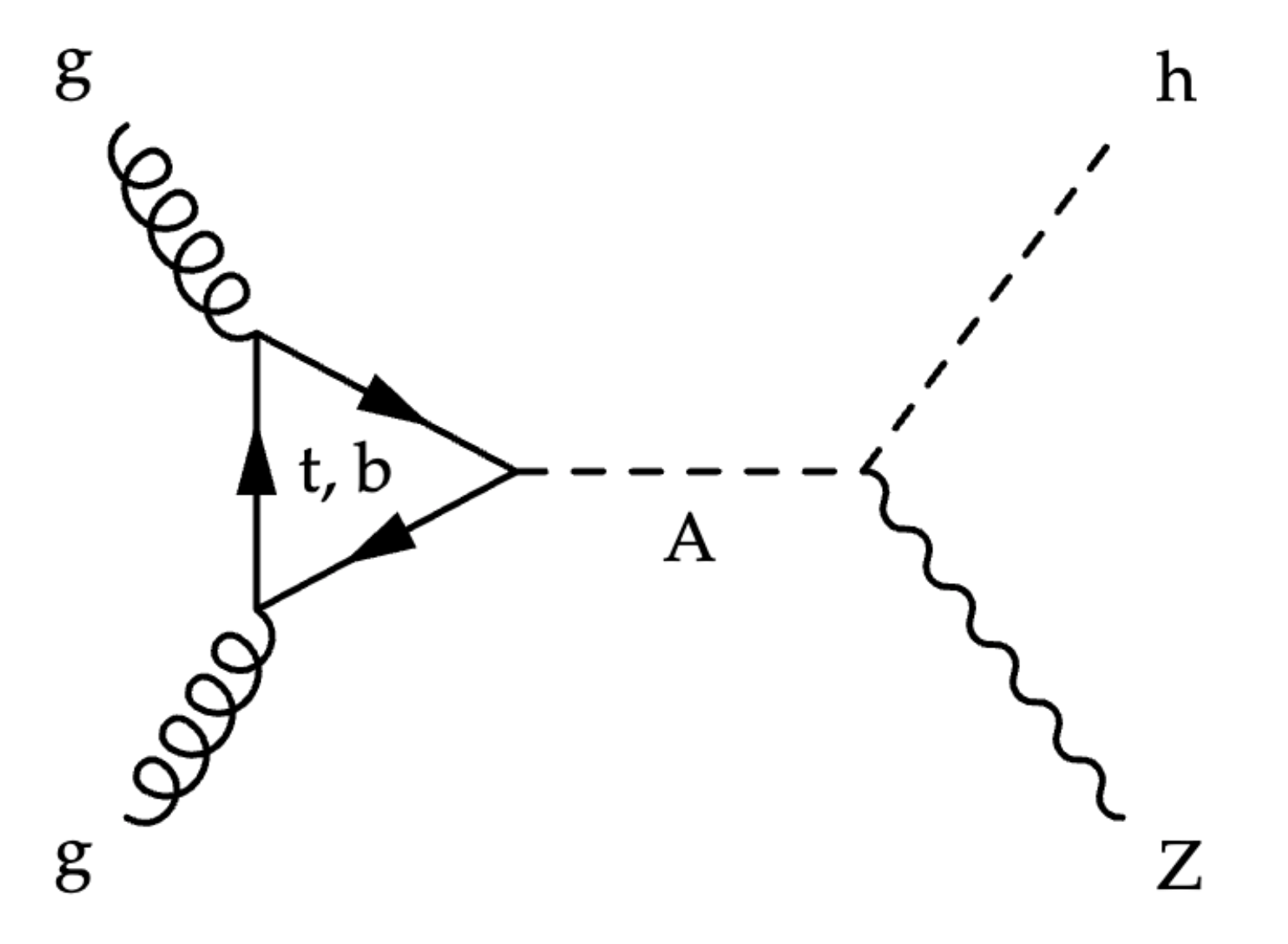
Figure 1: One way to produce an A is through gluon-gluon fusion. From left to right, two gluons “fuse” via a loop of heavy quarks (top t or bottom b), producing an A boson. The A then decays to Zh. These decays happen more-or-less instantaneously, so that none of these particles are observable in the detector. Instead, we look for the products of the Zh decay (ll𝜏𝜏 final states) and test their consistency with the pictured progenitors.

To complicate matters, a whole host of known Standard Model processes can produce events that look like ll𝜏𝜏. These processes constitute a background of events that obscures the A→Zh→ll𝜏𝜏 signal we seek. Our ability to separate signal from background hinges on a key variable, the mass m(ll𝜏𝜏) of the ll𝜏𝜏 system we observe. Imagine an ensemble of ll𝜏𝜏 events. We expect the masses of the background population to be broadly distributed across a range, without a strong preference for any particular value. On the other hand, if an A boson exists, we expect a well-defined peak in the distribution of m(ll𝜏𝜏) related to the mass of the upstream A boson. In effect, we are performing a so-called bump-hunt in the distribution of m(ll𝜏𝜏). If a bump exists, we must rigorously test its properties for consistency with an A boson. If we observe no bump, then we can set experimental constraints–statements falsifying the hypothesis that A bosons are produced with measurable couplings in the probed mass range–on theories predicting A bosons.

Figure 2: A CMS data event consistent with a Z decaying to two muons (red tracks depositing energy in the muon tracker) with a jet (yellow cone) and an electron (green track). The jet and electron are respectively consistent with leptonic and hadronic tau decays. The event was therefore selected as an A → Zh → ll𝜏𝜏 candidate with a reconstructed mass of m(ll𝜏𝜏) = 250.8 GeV.

So, what is it: discovery or tighter experimental constraints? Drum roll, please 🥁. 

Consistent with previous results, our analysis did not show any sign of an A boson in the distribution of m(ll𝜏𝜏). This is a null result, which can be roughly translated as, “if an A particle exists in the mass range we probed, it must be produced less frequently than what we are experimentally sensitive to.” In essence, we derived limits for the production of the A boson. These limits will inform theorists downstream about what a reasonable theory might predict. Because our analysis used the full CMS Run 2 dataset, corresponding to 138 fb-1 of data, in addition to the latest machine learning-based particle identification techniques, we have produced the most stringent limits on A→Zh measured in ll𝜏𝜏 final states to date. Our results coincide with recent results published by ATLAS, which used llbb final states (where h decays to bottom quarks b instead of taus) to place similar limits on the production of A. All hope is not lost for Beyond the Standard Model theories predicting additional Higgs bosons, though; they may simply exist at higher masses than we are experimentally sensitive to. It is for that reason that we look forward to future iterations of this analysis, and the new insights they may bring.

Figure 3: Supersymmetric models, if they are to accurately describe our universe, must be consistent with the properties of the observed Higgs boson, namely that mh = 125 GeV. One such supersymmetric model is named M(h,EFT)125. It is often parametrized by the mass of its A boson, mA, and a number related to the mass-generating mechanism in its extended Higgs sector, tan 𝛽. The results of our analysis–the non-observation of A–allow us to limit the possible values of mA and tan 𝛽, constraining the parameter space of M(h,EFT)125. In the figure, the area below the black dotted line is excluded; this area corresponds with range of (mA, tan 𝛽) consistent with the highest production of the A boson via gluon-gluon fusion (see Figure 1). This is no accident! Our limits are strongest where we are most likely to see a signal.

Read more about these results:

Date of publication
Tags / keywords
physics briefing
physics briefings

News